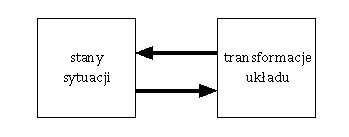
Jeżeli pomiędzy częściami układu dynamicznego występuje tego rodzaju oddziaływanie obiegowe, mówimy, że w układzie występuje s p r z ę ż e n i e z w r o t n e.

Taka definicja sprzężenia zwrotnego jest najbardziej zgodna z duchem niniejszej książki, która jest poświęcona przede wszystkim zagadnieniom zasadniczym.

Jednakże inne definicje są również możliwe i często dyskutuje się, która z nich jest najlepsza. Dlatego kilka słów wyjaśnienia może być przydatne. Istnieją dwa zasadnicze punkty widzenia, które należy rozpatrzyć.

Jedni – zgodnie z intencją tej książki – stawiają sobie za cel zrozumienie zasad licznych poszczególnych mechanizmów, które demonstrują te zasady. Dla nich „sprzężenie zwrotne” istnieje między dwiema częściami oddziaływającymi na siebie wzajemnie, jak to np. ma miejsce w układzie:

gdzie „i” jest symbolem i-tego stanu sytuacji lub i-tej transformacji układu.

Istotnie, wartości y w tym układzie wpływają na to, jak będzie zmieniać się x, a wartości x wpływają na y. Przeciwnie, nie można uważać, że sprzężenie zwrotne występuje w układzie:

gdyż w tym przypadku zmiana x nie zależy od wartości y; x dominuje nad y i działanie odbywa się tylko w jednym kierunku.

Drudzy – eksperymentatorzy i konstruktorzy – jako związani z praktyką pragną wykorzystać termin „sprzężenie zwrotne” (w tych przypadkach, gdy działanie wprost stanów sytuacji na wartości operacji można uznać za coś danego) na oznaczenie przekazywania pewnego zwrotnego oddziaływania wartości operacji na stany sytuacji za pośrednictwem pewnego powiązania, które jest fizycznie i materialnie oczywiste.

Występują oni przeciw definicji proponowanej przez matematyków, zwracając uwagę, że zmusza ona do stwierdzenia, że sprzężenie zwrotne występuje w zwykłym wahadle między jego momentem a pędem; takie „sprzężenie zwrotne” z praktycznego punktu widzenia jest czymś mistycznym. Na to odpowiada matematyk, że jeżeli będziemy brać pod uwagę obecność „sprzężenia zwrotnego” tylko wtedy, gdy przedstawiają je rzeczywiste przewody lub nerwy, teoria stanie się chaotyczna i pełna nieistotnych zastrzeżeń i ograniczeń.

W rzeczywistości jednak można zaniechać tych dysput, gdyż ścisła definicja sprzężenia zwrotnego w ogóle nie jest istotna. Natomiast faktem jest, że pojęcie „sprzężenia zwrotnego”, tak proste i naturalne w przypadkach elementarnych, staje się sztuczne i mało przydatne, gdy powiązania wzajemne między częściami stają się bardziej złożone.

Gdy rozpatrujemy tylko dwie części tak sprzężone, że oddziaływają na siebie wzajemnie, własności sprzężenia zwrotnego dają nam ważną i użyteczną informację o własnościach całości; lecz gdy liczba części wzrasta do kilku, powiedzmy czterech, i gdy każda z nich oddziaływa na trzy pozostałe, wtedy można wyznaczyć dwadzieścia obiegów zamkniętych; jednakże znajomość własności wszystkich tych dwudziestu obiegów nie daje jeszcze pełnej informacji o układzie. Takich złożonych układów nie można traktować jako splątanego zbioru mniej lub bardziej niezależnych obiegów sprzężenia zwrotnego, lecz należy go traktować wyłącznie jako całość.

Zatem dla zrozumienia ogólnych zasad układów dynamicznych pojęcie sprzężenia zwrotnego jest samo w sobie niewystarczające. Istotne jest jedynie to, że układy złożone o licznych wewnętrznych powiązaniach skrośnych mają złożony sposób zachowania się i że ten sposób zachowania się może być celowy w złożonych sytuacjach.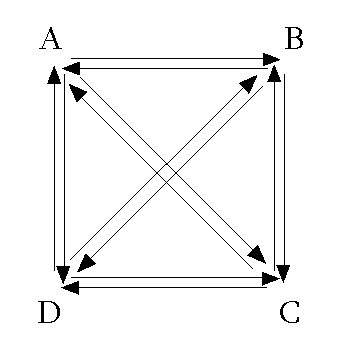